Puzzle: The Riddler Mar 06 - Guess Who

Mar 19, 2020 #monte-carlo

In the game of “Guess Who,” each player first randomly (and independently of their opponent) selects one of N character tiles. While it’s unlikely, both players can choose the same character. Each of the N characters is distinct in appearance — for example, characters have different skin tones, hair color, hair length and accessories like hats or glasses.

Each player also has access to a board with images of all N characters. The players alternate taking turns, and during each turn a player has two options:
Make a specific guess as to their opponent’s selected character. If correct, the player who made the guess immediately wins. Otherwise, that player immediately loses.

Ask a yes-or-no question about their opponent’s chosen character, in order to eliminate some of the candidates. Importantly, if only one possible character is left after the question, the player must still wait until their next turn to officially guess that character.

Assume both players are highly skilled at choosing yes-or-no questions, so that they can always craft a question to potentially rule out (or in) any desired number of candidates. Also, both are playing to maximize their own probability of winning.

Let’s keep things (relatively) simple, and suppose that N = 4. How likely is it that the player who goes first will win?

Extra credit: If N is instead 24 (the number of characters in the original “Guess Who” game), now how likely is it that the player who goes first will win?

Extra extra credit: If N is instead 14, now how likely is it that the player who goes first will win?

For N = 4, the optimal strategy here is to ask a question which narrows the choices down to 1. If you get it, you force your opponent to make a wild guess in the next round. The purpose of this post is not to solve for N but provide an exploratory experiment into the general solution.

## pseudo code ---- 

1. The game has N characters and 2 players (A, B);
2. Both players start with a winning chance (theta) of 1/N;
3. At every round, 
    3.1 check opponent's theta. If opp's theta is 1, makes a random guess, else do,
    3.2 choose x over vector(1 to N). If x == 2 (2 characters remaining), theta => 1, else nothing;
4. Round done, N - 1;

# optimal strategy = asymmetry elimination
optimal_guess <- function(vec, target, split, frac = 1) {
    
    # toggle between mode: adjust split directly or fraction
    if (is.integer(split)) {
        pick = sample(vec, ceiling(split * frac))
    } else if (frac < 1) {
        x = max(ceiling(length(vec) * frac), 1)
        pick = sample(vec, x)
    } else {
        stop("Must specify split or fraction")
    }
    
    # if range is right, pick this side
    if (target %in% pick) return(pick);
    
    # else pick another side
    setdiff(vec, pick)
}

# wrapper to check if player gets it
correct_guess <- function(vec, target) {
    all(vec == target, na.rm = TRUE)
}

run_game <- function(A, B, split, frac) {
  
    # A's turn knowing B will win next round
    if (correct_guess(B, "B")) {
        return( ifelse(correct_guess(sample(A, 1), "A"), "A", "B") )
    }
    
    # A's turn
    A.guesses = optimal_guess(A, "A", split, frac)
    
    # B's turn knowing A will win next round,
    # make a random guess
    if (correct_guess(A.guesses, "A") | length(A) == 2) {
        return( ifelse(correct_guess(sample(B, 1), "B"), "B", "A") )
    }
    
    # B's turn 
    B.guesses = optimal_guess(B, "B", split, frac)
    
    # this round done, continue next
    run_game(A.guesses, B.guesses, split, frac)
}

run_game simulates a single round game. I enable 2 modes here, using split for splitting with absolute number or frac for splitting with portion of remainings. The latter is for further investigation we will be doing later.

# generate data
set.seed(1212)
N = 4
init = sample(LETTERS[1:N], N)

# mode 1: using absolute fixed split
run_game(init, init, split = 1L, frac = 1)

## [1] "A"

# mode 2: using fraction of remaining
run_game(init, init, split = NA, frac = 0.3)

## [1] "A"

The game works. Now, we are ready solve for N is 4 by running simulation.

# run simulation
mean(replicate(100e3, run_game(init, init, split = 1L, frac = 1)) == "A")

## [1] 0.56246

The answer is 56.25% for N = 4. For small N, one can probably deduce the answer logically. 25% of the time A forces B to guess at first round which gives 75% of winning probability. 75% of the time both has equal chances. Thus,

\[ (0.25 * 0.75) + (0.75 * 0.5) = 0.5625 \]

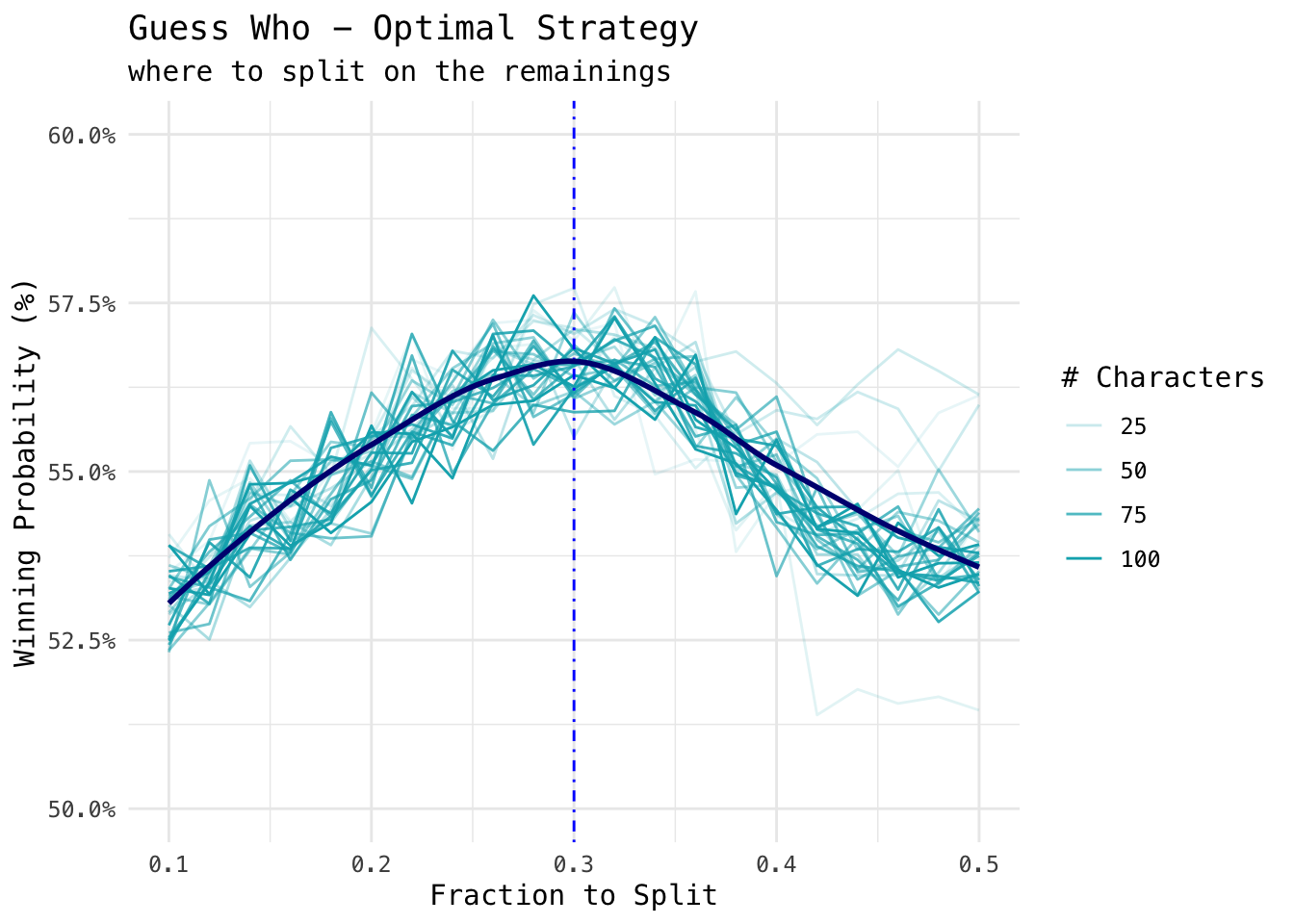
For N = 14, 24, and etc., the logical deduction becomes almost impossible. To investigate optimal strategy to play the game for various N, we simulate multiple combinations. This is solely for exploratory purposes because it has a fundamental flaw. We assume both players always carry the same strategy and do not adjust for the characters remaining as the game progresses.

library(tidyverse)
library(furrr)

set.seed(1212)
# run in parallel
future::plan(strategy = "multiprocess")

# random sample number of possible characters in the game
nn = sort(sample(10:100, 30))
# game strategy (fraction to split)
fr = seq(0.1, 0.5, 0.02)

# a wrapper to run combination of N and frac for `run game` 
simulate_this <- function(N, fracs, trials = 3000) {
  future_map_dbl(fracs, ~ {
    init = sample(LETTERS[1:N], N)
    outs = replicate(trials, run_game(init, init, split = NA, frac = .x))
    mean(outs == "A")
  })
}

res <- purrr::map(nn, ~ simulate_this(N = .x, fr = fr, trials = 10e3))

tidy_res <- res %>% 
  as.data.frame() %>% 
  set_names(nn) %>% 
  bind_cols(fraction = fr) %>% 
  gather(N, prob, -fraction) %>% 
  mutate(N = as.numeric(N)) %>% 
  as_tibble()
tidy_res

## # A tibble: 630 x 3
##    fraction     N  prob
##       <dbl> <dbl> <dbl>
##  1     0.1     12 0.535
##  2     0.12    12 0.540
##  3     0.14    12 0.554
##  4     0.16    12 0.554
##  5     0.18    12 0.551
##  6     0.2     12 0.555
##  7     0.22    12 0.567
##  8     0.24    12 0.564
##  9     0.26    12 0.572
## 10     0.28    12 0.572
## # … with 620 more rows

tidy_res %>% 
  ggplot(aes(fraction, prob, alpha = N, group = N)) + 
  geom_line(col = "#00AFBB") + 
  scale_y_continuous(limits = c(0.5, 0.6), labels = scales::percent) +
  scale_color_brewer(type = "seq") +
  geom_vline(xintercept = 0.3, lty = 4, col = "blue") +
  geom_smooth(aes(group = 1), method = "loess", se = FALSE,
              col = "navyblue", show.legend = FALSE) +
  theme_minimal(base_family = "Menlo") + 
  labs(x        = "Fraction to Split", 
       y        = "Winning Probability (%)", 
       alpha    = "# Characters",
       title    = "Guess Who - Optimal Strategy",
       subtitle = "where to split on the remainings")