Puzzle: Biased Coin Toss

Apr 21, 2019 #monte-carlo

From this paper “What’s Past Is Not Prologue” comes a quiz,

You are presented with two coins: one is fair, and the other has a 60% chance of coming up heads. Unfortunately, you don’t know which is which. How many flips would you need to perform in parallel on the two coins to give yourself a 95% chance of correctly identifying the biased one?

The following demonstrates 2 simulation methods to obtain the result.

library(tidyverse)
library(ggthemes)
library(discreteRV)
set.seed(1212)

# ggplot theme
old <- theme_set(theme_tufte() + theme(text = element_text(family = 'Menlo')))

# limit range from 50 to 200 flips
flips  = 50:200
trials = 3000

# Method One --------------------------------------------------------------


# actually simulate the action of tossing 2 coins
method_one <- function(x) {
    regular = rbinom(x, 1, .5)
    biased  = rbinom(x, 1, .6)
    # return
    sum(biased) - sum(regular)
}

# repeat action and bind into a data frame
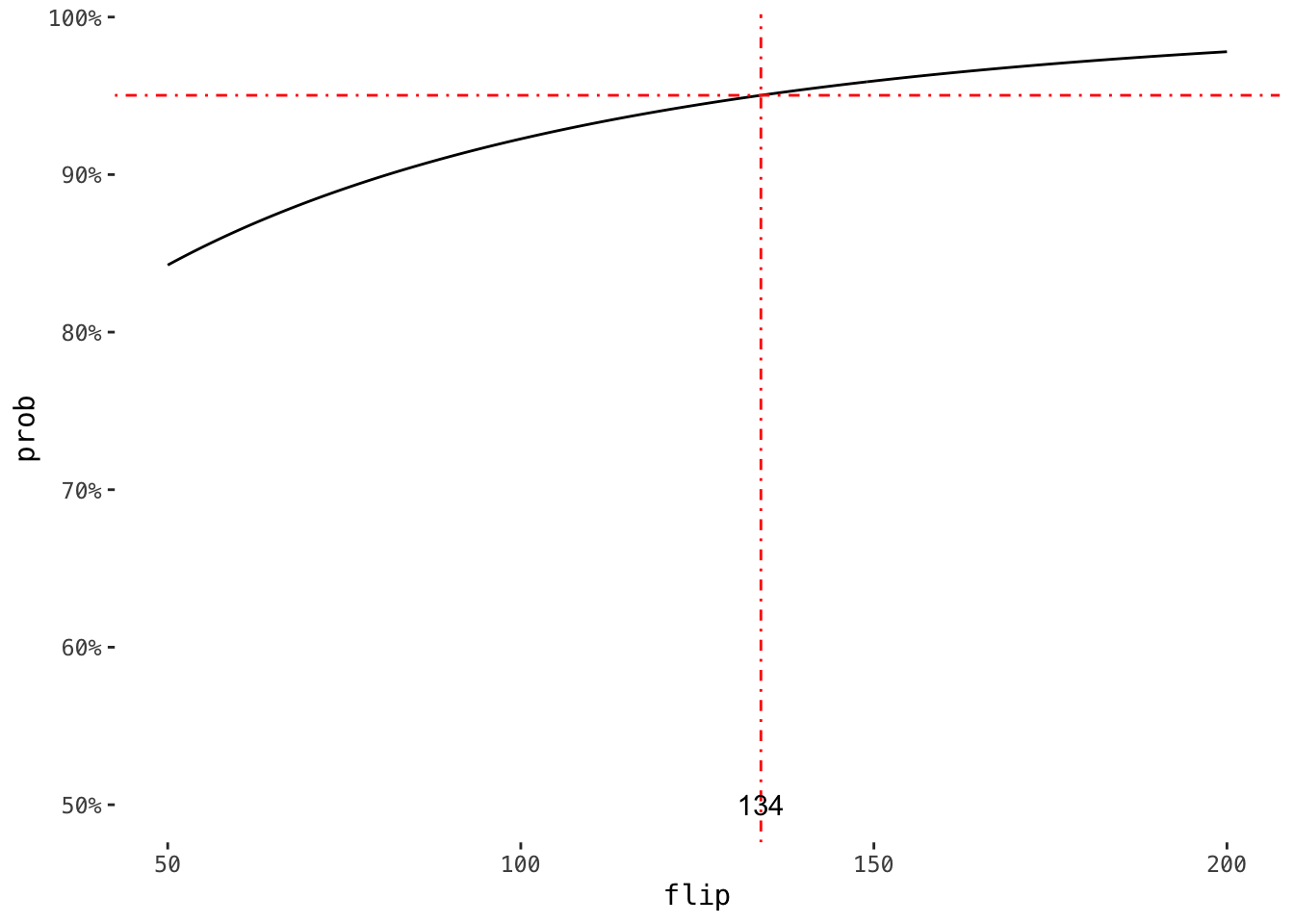
res_method_one <-
    map_dbl(flips, ~ {
        sum(replicate(trials, method_one(.x)) > 0) / trials
    }) %>%
    bind_cols(flip = flips, prob = .)

# first occurance
min_flip_of_method_one <-
    res_method_one %>%
    filter(prob >= 0.95) %>%
    slice(1)

# visualize result
res_method_one %>%
    ggplot(aes(flip, prob)) +
    geom_line() +
    geom_vline(xintercept = min_flip_of_method_one$flip, lty = 4, col = "red") +
    geom_hline(yintercept = min_flip_of_method_one$prob, lty = 4, col = "red") +
    annotate(
        "text",
        x = min_flip_of_method_one$flip,
        y = .5,
        label = as.character(min_flip_of_method_one$flip)
    ) +
    scale_y_continuous(breaks = seq(.5, 1, .1), labels = scales::percent)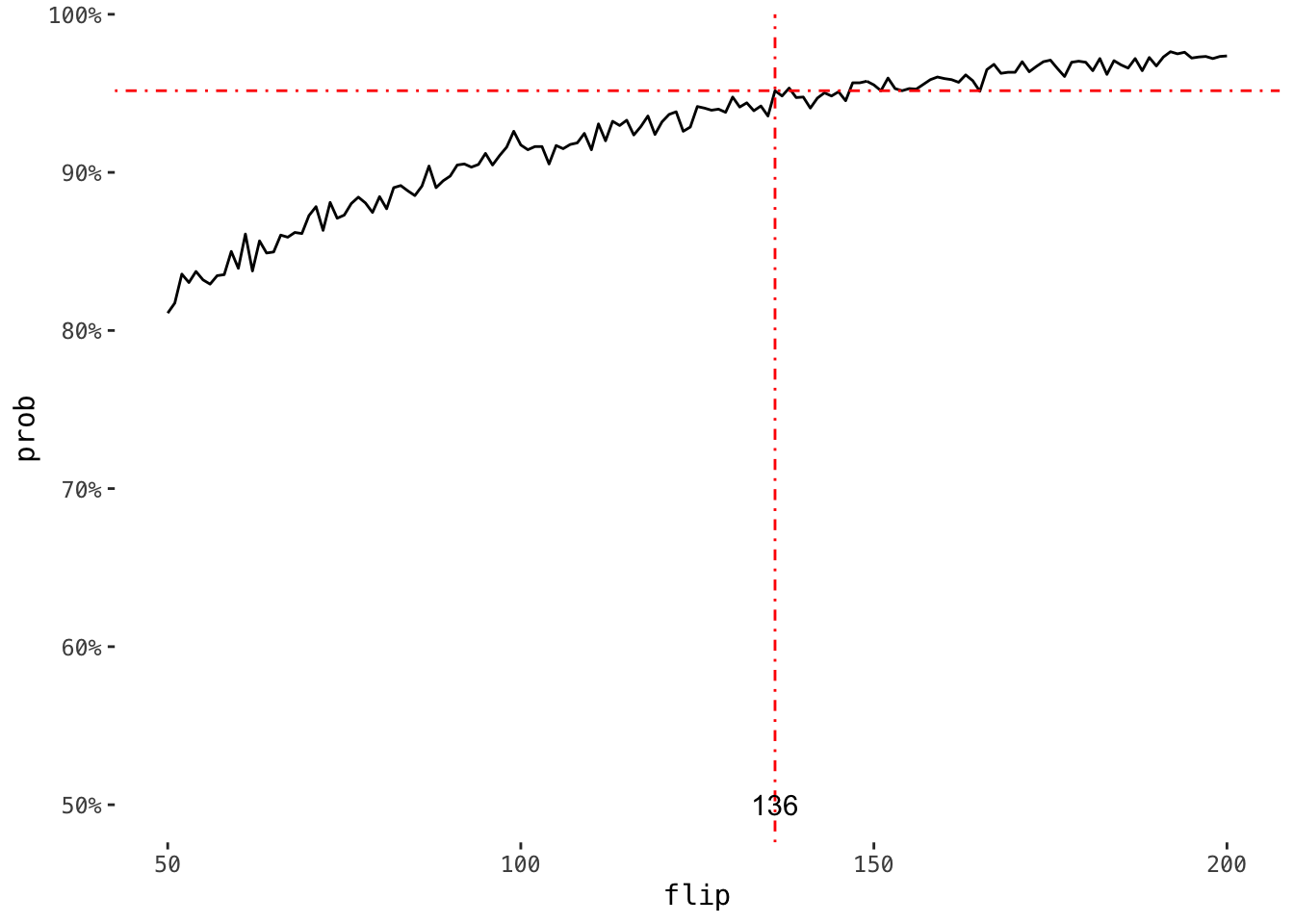

# Method Two --------------------------------------------------------------


# we will reuse this function repeatedly to test different diff flips
method_two <- function(x) {
    
    # how many tosses?
    regular = RV(1:x, dbinom(1:x, size = x, prob = .5))
    biased  = RV(1:x, dbinom(1:x, size = x, prob = .6))
    
    # joint pmf
    jpmf <- joint(regular, biased)
    
    # probability = proportion of combination of possible outcomes
    tibble(prob = probs(jpmf), comb = outcomes(jpmf)) %>%
        separate(comb, c("fair", "biased"), ",", convert = TRUE) %>%
        # if biased lands more than unbiased coin, choose correctly
        # if both lands the same, choose randomly
        mutate(correct = case_when(biased >  fair ~ 1.0,
                                   biased == fair ~ 0.5,
                                   biased <  fair ~ 0.0)) %>%
        # the likelihood that guessing correctly happens
        mutate(likelihood = prob * correct) %>%
        filter(correct > 0) %>%
        summarise(conf = sum(likelihood)) %>%
        pull(conf)

}

# loop thru flips
res_method_two <- 
    flips %>% 
    map_dbl( ~ method_two(.x) ) %>% 
    bind_cols(flip = flips, prob = .)

# minimum flip to obtain 95% confidence
min_flip_of_method_two <- 
    res_method_two %>%
    filter(prob >= 0.95) %>%
    slice(1)

res_method_two %>%
    ggplot(aes(flip, prob)) +
    geom_line() +
    geom_vline(xintercept = min_flip_of_method_two$flip, lty = 4, col = "red") +
    geom_hline(yintercept = min_flip_of_method_two$prob, lty = 4, col = "red") +
    annotate(
        "text",
        x = min_flip_of_method_two$flip,
        y = .5,
        label = as.character(min_flip_of_method_two$flip)
    ) +
    scale_y_continuous(breaks = seq(.5, 1, .1), labels = scales::percent)