Pseudo R Squared

Nov 26, 2018 #descr

library(tidyverse)
library(descr)

# make reproducible 
set.seed(1234)
# number of points
nn <- 100

# An Simulated Model --------------------------------------------------------

# simulate binary response
y <- rbinom(nn, 1, prob = .5)
# single predictor
x <- y + rnorm(nn, mean = 1, sd = .5)
cor(x, y)

## [1] 0.7404515

# null model (without any predictor)
null_mod <- glm(y ~  1, family = "binomial")
# we know x is inheritly random
some_mod <- glm(y ~ x, family = "binomial")

# glance 
summary(some_mod)

## 
## Call:
## glm(formula = y ~ x, family = "binomial")
## 
## Deviance Residuals: 
##      Min        1Q    Median        3Q       Max  
## -2.09191  -0.31476  -0.06342   0.43491   1.85033  
## 
## Coefficients:
##             Estimate Std. Error z value Pr(>|z|)    
## (Intercept)  -7.9100     1.5971  -4.953 7.32e-07 ***
## x             4.9034     0.9643   5.085 3.68e-07 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## (Dispersion parameter for binomial family taken to be 1)
## 
##     Null deviance: 137.63  on 99  degrees of freedom
## Residual deviance:  59.99  on 98  degrees of freedom
## AIC: 63.99
## 
## Number of Fisher Scoring iterations: 6

# the same result
1 - logLik(some_mod) / logLik(null_mod)

## 'log Lik.' 0.5641121 (df=2)

1 - some_mod$deviance / some_mod$null.deviance

## [1] 0.5641121

# from package
descr::LogRegR2(some_mod)

## Chi2                 77.63748 
## Df                   1 
## Sig.                 0 
## Cox and Snell Index  0.5399292 
## Nagelkerke Index     0.7223295 
## McFadden's R2        0.5641121

# Pseudo Rsq ~ Predictor Power ------------------------------------------

# vary predictor power by adding various degree of deviation
# return a list of int vector
ints <- map(seq(.1, .8, .01), ~ y + rnorm(nn, mean = 1, sd = .x))

# fit and extract pseudo rsq
get_pseudo_rsq <- function(vec) {
  fit <- glm(y ~ vec, family = "binomial")
  pseudo_rsq <- LogRegR2(fit)
  # return
  with(pseudo_rsq, list(
    corr = cor(vec, y),
    `McFadden` = RL2,
    `Cox & Snell` = CoxR2,
    `Nagelkerke` = NagelkerkeR2
  ))
} 
rsqs <- map(ints, get_pseudo_rsq)

# visualize corresponding pseudo rsq by correlation
rsqs %>% 
  bind_rows() %>% 
  gather(met, rsq, -corr) %>% 
  ggplot(aes(corr, rsq, col = met)) + 
  geom_line() + 
  geom_hline(yintercept = .5, col = "darkgray", lty = 3) + 
  theme_minimal(base_family = "Menlo") + 
  labs(x = "Correlation", y = "Pseudo R Squared", col = "Variant")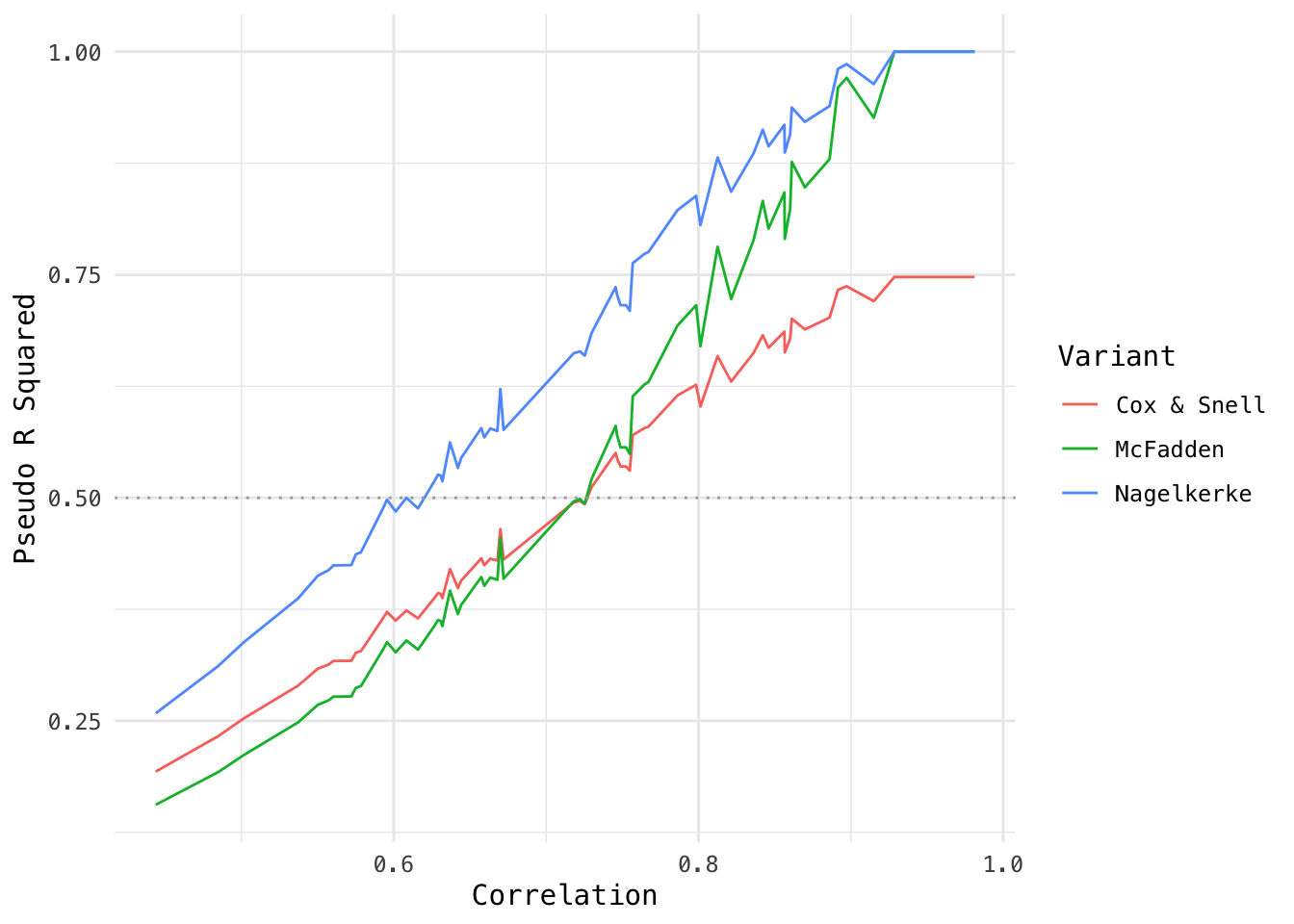

For more info, see https://stats.idre.ucla.edu/other/mult-pkg/faq/general/faq-what-are-pseudo-r-squareds/